Nếu đã tìm hiểu về machine learning, chắc bạn cũng không còn xa lạ với khái niệm Loss function. Nhưng thực thế không có nhiều người hiểu được cụ thể Loss function là gì? Những thông tin liên quan tới Loss function? Trong bài viết ngày hôm nay hãy cùng topviecit.vn tìm hiểu câu trả lời cho câu hỏi này nhé!
Loss function là gì?
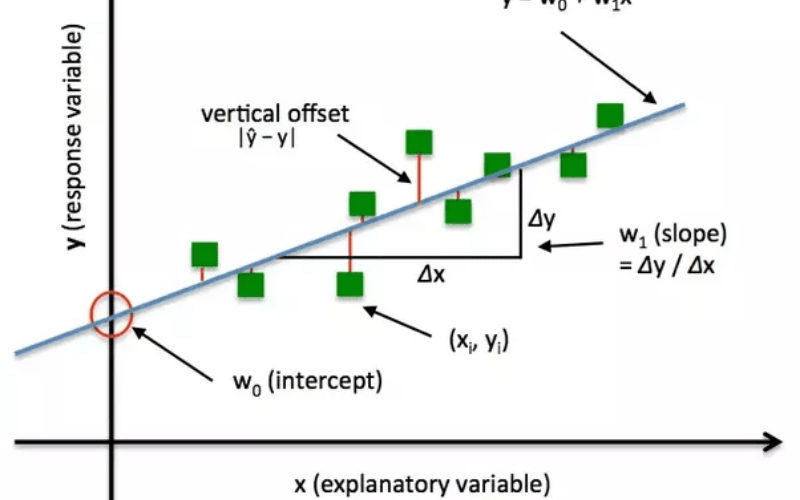
Loss function là gì? Loss function được gọi là hàm mất mát trong tiếng Việt, nó thể hiện mối quan hệ giữa y (là giá trị thực tế) và y* (là kết quả dự đoán của model). Cụ thể hàm mất mát sẽ có dạng như sau: f(y) = (y* – y)^2.
Ở các thuật toán tìm kiếm của trí tuệ nhân tạo cổ điển, hàm loss được coi là một hàm mục tiêu của quá trình tìm kiếm giúp thực hiện các thay đổi hay phương pháp di chuyển sao cho hàm mục tiêu có giá trị nhỏ nhất hoặc chấp nhận được.
Trong lĩnh vực học máy ham được đưa vào với mục đích là để tối ưu tối ưu tối nhất model của mình, đồng thời cũng là để đánh giá độ tốt của model ( y* càng gần y thì càng tốt).
Hiểu đơn giản chính là dựa vào hàm mất mát ta có thể tính ra gradient descent nhằm mục đích tối ưu loss function càng về gần 0 càng tốt.
Tìm hiểu thêm: Hadoop Là Gì? Tìm Hiểu Chi Tiết Về HDFS
Cách xây dựng Loss function là gì?
Cách xây dựng Loss function là gì? Loss function được dùng để đo đạc chênh lệch giữa $$y$$ và $$\hat{y}$$, sự chênh lệch chính là hiệu của chúng.
Cụ thể, $$ L(\hat{y}, y) = \hat{y} \ – \ y
$$
Thực tế hàm này lại không đáp ứng được tính chất không âm của một loss function. Do vậy ta phải lấy giá trị tuyệt đối của hiệu này:
$$ L(\hat{y}, y) = |\hat{y} – y|
$$
Hiệu này thỏa mãn tính chất không âm, nhưng lại không dễ để cực tiểu hóa, lý do là bởi đạo hàm của nó không liên tục ( đạo hàm của $$f(x) = |x|$$ đứt quãng tại $$x = 0$$), trong khi các phương pháp cực tiểu hóa hàm số thông dụng lại hoàn toàn có thể tính được đạo hàm. Chúng ta còn có một phương pháp tính khác đó là bình phương của hiệu. Cụ thể là:
$$ L(\hat{y}, y) = \frac{1}{2}(\hat{y} – y)^2
$$
Nếu đạo hàm được tính theo $$\hat{y}$$, công thức sẽ là $$\nabla L = \frac{1}{2} \times 2 \times (\hat{y} – y) =\hat{y} – y$$. Trong đó ta thấy hằng số $$\frac{1}{2}$$ không có hằng số phụ, xuất hiện chỉ nhằm mục đích cho đạo hàm trông đẹp mắt mà thôi. Người ta gọi loss function này là square loss, nó sử dụng cho cả regression và classification, nhưng có vẻ regression chiếm ưu thế hơn.
Với binary classification, bạn vẫn còn một cách tiếp cận khác nữa để xây dựng loss function. Ở dạng bài này trường hợp model trả về $$\hat{y} < 0$$ kết quả sẽ là -1, còn nếu trả về $$\hat{y} \geq 0$$ thì đáp án là +1.
Loss function của binary classification phải đáp ứng một số tiêu chí sau:
- Phạt model nhiều lên khi chúng dự đoán sai và giảm đi khi chúng dự đoán đúng. Nếu model dự đoán sai ($$y$$ khác dấu với $$\hat{y}$$) thì loss function sẽ có giá trị được trả về lớn hơn khi model đúng ($$y$$ cùng dấu với $$\hat{y}$$).
- Trong trường hợp có cả hai đáp án $$\hat{y}_1$$ và $$\hat{y}_2$$ đều cùng dấu thì phương án được thích là phương án đúng, model càng thích thì sẽ được khuyến khích và phạt ít hơn. Còn khi khác dấu phương án được thích là phương án sai nên model càng thích thì càng phải phạt nặng để nó không lặp lại lỗi sai đó nữa.
Tóm lại, với binary classification thì các loss function có công thức tổng quát như sau:
$$ L(\hat{y}, y) = f(y \cdot \hat{y})
$$
( Mà trong đó $$f$$ là hàm không âm cũng chẳng tăng).
Tìm hiểu thêm: Học IT Có Khó Không? Cơ Hội Việc Làm Của Ngành IT Sau Khi Ra Trường?
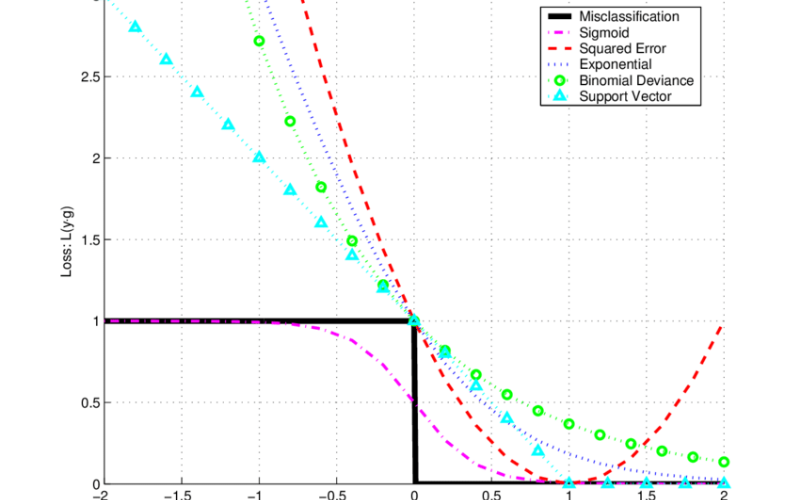
Một số loss function cơ bản dành cho binary classification
Dưới đây là những loss function cơ bản cho binary classification là:
0-1 loss
Hàm này sẽ trả đáp án về 1 trong trường hợp $$y \cdot \hat{y} < 0$$, và trả đáp án về 0 khi ngược lại. Bản chất của điều này tương tự như đếm số câu trả lời sai của model.
Hàm 0-1 loss sẽ được dùng để tính error rate của model chứ không dùng cho mục đích huấn luyện model tại vì đạo hàm của nó không nằm ở 0.
Perceptron loss
Có dạng như sau:
$$ L_{perceptron}(\hat{y}, y) = \max(0,- y \cdot \hat{y})
$$
Hàm này giúp sửa sao cho hàm $$g$$ trở thành không âm (điều kiện của hàm mất mát).
Nếu model đoán đúng ($$\hat{y}$$ cùng dấu với $$y$$), $$- y \cdot \hat{y}$$ sẽ âm, tức là perceptron loss không thể phân biệt giữa các dự đoán đúng, nên sẽ không xảy ra hiện tượng phạt. Còn với dự đoán sai, thì perceptron vẫn tuân thủ quy tắc model càng thích thì phạt càng nặng.
Hinge loss
Có dạng tổng quát như sau:
$$ L_{hinge}(\hat{y}, y) = \max(0, 1 – y \cdot \hat{y})
$$
Hinge loss chính là một biến thể từ perceptron loss. Điểm khác là đơn vị vào đại lượng $$- y \cdot \hat{y}$$ được thêm vào, gọi tắt là margin (lề).
Không khó để nhận ra hinge loss hoạt động gần giống perceptron loss, ngoại trừ các dự đoán mà $$y \cdot \hat{y}$$ trong khoảng $$[0, 1]$$ ( Dự đoán $$y \cdot \hat{y}$$ ở trong khoảng này đều sẽ đúng).
Hinge loss phân biệt dự đoán đúng, theo nguyên tắc model càng thích thì càng phạt nhẹ. Khi $$y \cdot \hat{y}$$ > 1 thì chúng không thể phân biệt các dự đoán nữa.
Lý do cho điều này chính là dự đoán ở trong margin $$[0, 1]$$ là những dự đoán gần ranh giới, model đang lưỡng lự. Mà hinge loss đòi hỏi model phải thật rõ ràng, tự tin vào quyết định của nó để có thể đưa ra những quyết định có tính chắc chắn cao.
Logistic loss (hay log loss)
Có dạng tổng quát như sau:
$$ L_{log}(\hat{y}, y) = \log_2(1 + \exp(- y \cdot \hat{y}))
$$
Theo công thức trên, hàm $$\exp(\cdot)$$ là hàm lũy thừa với cơ số $$e$$. Log loss mang tới cảm giác phức tạp và không giống với những hàm còn lại. Nhưng thực tế nó thỏa mãn tất cả mọi tính chất của loss function.
Hàm này có tính liên tục, không âm và không tăng. Thậm chí nó còn có xu hướng giảm, tức là nó có khả năng phân biệt giữa các dự đoán có độ thích khác nhau bất kể đúng hay sai. Ngoài ra điểm khác biệt nữa nằm ở việc hàm này có một độ cong nhất định, hiểu đơn giản chính là không giảm dù tốc độ như nhau ở mọi điểm.
Tìm hiểu thêm: SRE Là Gì? Khác Biệt Giữa SRE Và DevOps
Có lẽ qua bài viết trên bạn đã phần nào hiểu được Loss function là gì? Và những thông tin xoay quanh nó. Hy vọng thông tin trên hữu ích cho bạn! Và đừng quên truy cập ngay vào TopCV để cập nhật việc làm IT liến quan đến Loss function mỗi ngày!
Có thể bạn quan tâm: Tester là gì? Tester là làm gì? Mô tả chi tiết công việc
Hình ảnh: Sưu tầm